|
|
|
|
 | |  |
| If the midpoint of the hypotenuse of a right triangle is equidistant from each of the vertices of a the triangle, the triangle must be an isosceles right triangle? | |
 | |  |
|
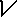
 |
 | |  |
| If you make a triangle ABC and B is the right angle and the midpoint is D, then you have AD, DC and BD all the same length. | |
 | |  |
|

|
|
|
|
|
|
 | |  |
| So AD, DC and BD will be x. We need to find what AB and BC are. Since BD bisects AC, we get two new right angle at BDC and BDA. So if we use pythagorean theorem, BD and AD squared equals AB squared. | |
 | |  |
|
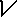
 |
 | |  |
| If you work it out you get AB is the square root of 2x squared. When you sub in a number like 2 for example you get side AB equals the square root of 8. | |
 | |  |
|

|
|
|
|
|
|
 | |  |
| The other side BC is the same formula so it is alos the square root of 8. So if we use pythagorean again it is 8+8=AC squared. So it is square root of 16 which is 4. | |
 | |  |
|
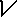
 |
 | |  |
| Which means we have an isosceles triangle always. | |
 | |  |
|

|
|